Journal:Acta Cryst D:S2059798320011869
From Proteopedia
(Difference between revisions)

| Line 17: | Line 17: | ||
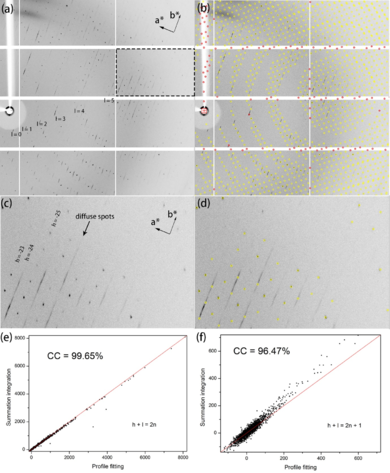
This randomness breaks the long-term periodic and forms a local short-term periodic. This appears to be the particle-size broadening (Coppens, 1997)<ref name="Coppens">PMID:25727874</ref>. If the long-term periodic is broken, the diffraction intensity would spread along the reciprocal-space direction of the step function. In this special case, it is the b* direction. With the spread of the reflections, the subsidiary maxima of the neighboring reflections may overlap, which will result in the smear spots, the especial chacteracters of LTD. | This randomness breaks the long-term periodic and forms a local short-term periodic. This appears to be the particle-size broadening (Coppens, 1997)<ref name="Coppens">PMID:25727874</ref>. If the long-term periodic is broken, the diffraction intensity would spread along the reciprocal-space direction of the step function. In this special case, it is the b* direction. With the spread of the reflections, the subsidiary maxima of the neighboring reflections may overlap, which will result in the smear spots, the especial chacteracters of LTD. | ||
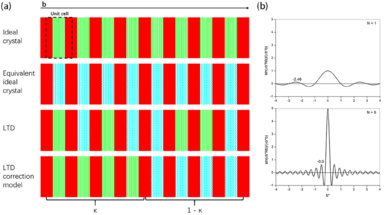
| - | In the intensity deconvolution methods, the randomly distributed two different kinds of layers (third in Fig. 6a) were supposed to accumulate into two mosaic domains (fourth in Fig. 6a), which is similar to twining (Dauter & Jaskolski, 2016)<ref name="Dauter">PMID:28132496</ref>. The corrected intensities could be obtained by dividing the observed value by the factor of [(2''k''<sup>2</sup>-2k+1)+2k(1-k)cos(2πh''t''<sub>d</sub>)]. Therefore, LTD problem could be solved. | + | In the intensity deconvolution methods, the randomly distributed two different kinds of layers (third in Fig. 6a; see static image below) were supposed to accumulate into two mosaic domains (fourth in Fig. 6a), which is similar to twining (Dauter & Jaskolski, 2016)<ref name="Dauter">PMID:28132496</ref>. The corrected intensities could be obtained by dividing the observed value by the factor of [(2''k''<sup>2</sup>-2k+1)+2k(1-k)cos(2πh''t''<sub>d</sub>)]. Therefore, LTD problem could be solved. |
[[Image:Figure_6.png|thumb|390px|left|'''Figure 6''' A lattice-translocation defect model. (a) The lattice has a layer structure with layers (parallel to the ac plane) stacked along the b direction. (b) The particle-size broadening introduced by the finite unit-cell translations.]] | [[Image:Figure_6.png|thumb|390px|left|'''Figure 6''' A lattice-translocation defect model. (a) The lattice has a layer structure with layers (parallel to the ac plane) stacked along the b direction. (b) The particle-size broadening introduced by the finite unit-cell translations.]] | ||
Revision as of 11:26, 21 September 2020
| |||||||||||
This page complements a publication in scientific journals and is one of the Proteopedia's Interactive 3D Complement pages. For aditional details please see I3DC.