Lattice-translocation defects in some specific crystals of the catalytic head domain of influenza neuraminidase
Linghui Li, Shuliu Dai, George F. Gao and Jiawei Wang [1]
Molecular Tour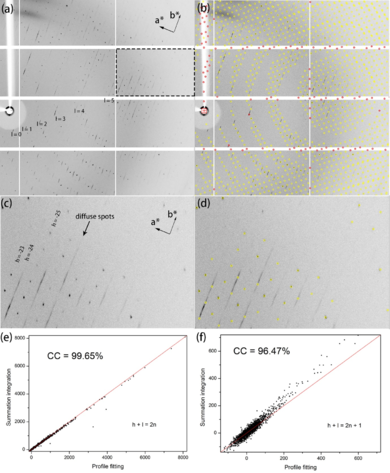
The globular tetrameric properties of neuraminidase (NA) heads might produce crystals with pathological imperfections—lattice-translocation defects (LTD)—which make the structure determination not straightforward anymore. In this report, using the crystal of the NA head from the Wuhan Asiatic toad influenza virus as an example, the identification and solution for this kind of crystal pathology are presented. Furthermore, its underlying mechanism of formation was explored.
Figure 1 The first image of diffraction data of a toad NA crystal. (a) Raw image with the reciprocal-space index l shown, as well as the a* and b* axes. (b) The same image with all predictions shown. (c) The enlarged section of the frame in (a) with the h index shown. The smeared diffuse spots are indicated with an arrow. (d) The enlarged section with predictions larger than 5 σ shown. (e) The correlation of spot intensities integrated with profile fitting and summation methods with the indexes (h+l) of even, (f) (h+l) odd.
In the lattice-translocation defect crystals, every other layer is either in the Fig. 5b orientation or in the , and the choice is absolutely random. This randomness breaks the long-term periodic and forms a local short-term periodic. This appears to be the particle-size broadening (Coppens, 1997)[2]. If the long-term periodic is broken, the diffraction intensity would spread along the reciprocal-space direction of the step function. In this special case, it is the b* direction. With the spread of the reflections, the subsidiary maxima of the neighboring reflections may overlap, which will result in the smear spots, the especial chacteracters of LTD.
In the intensity deconvolution methods, the randomly distributed two different kinds of layers (third in Fig. 6a) were supposed to accumulate into two mosaic domains (fourth in Fig. 6a), which is similar to twining (Dauter & Jaskolski, 2016)[3]. The corrected intensities could be obtained by dividing the observed value by the factor of [(2k2-2k+1)+2k(1-k)cos(2πhtd)]. Therefore, LTD problem could be solved.
References
- ↑ Li L, Dai S, Gao GF, Wang J. Lattice-translocation defects in specific crystals of the catalytic head domain of influenza neuraminidase. Acta Crystallogr D Struct Biol. 2020 Nov 1;76(Pt 11):1057-1064. doi:, 10.1107/S2059798320011869. Epub 2020 Oct 13. PMID:33135677 doi:http://dx.doi.org/10.1107/S2059798320011869
- ↑ Michael JR, Volkov A. Density- and wavefunction-normalized Cartesian spherical harmonics for l </= 20. Acta Crystallogr A Found Adv. 2015 Mar;71(Pt 2):245-9. doi:, 10.1107/S2053273314024838. Epub 2015 Jan 23. PMID:25727874 doi:http://dx.doi.org/10.1107/S2053273314024838
- ↑ Dauter Z, Jaskolski M. Crystal pathologies in macromolecular crystallography. Postepy Biochem. 2016;62(3):401-407. PMID:28132496
